align_planes::align
Creates a transformation that changes from one plane to another plane.
Signatures
- align( vector vecA1, vector vecA2, vector vecB1, vector vecB2 )
- align( vector vecA1, vector vecA2, vector originA, vector vecB1, vector vecB2, vector originB )
Details
The transformation created by the function transforms from a plane A into another plane B. Each of the planes is defined by two non-linear in-plane vectors (i.e. the basis vectors of the planes) and eventually by an origin point (see description on wikipedia). For best function, the two pairs of in-plane vectors should form similar triangles. The vectors of each pair are not required to be orthonormal.
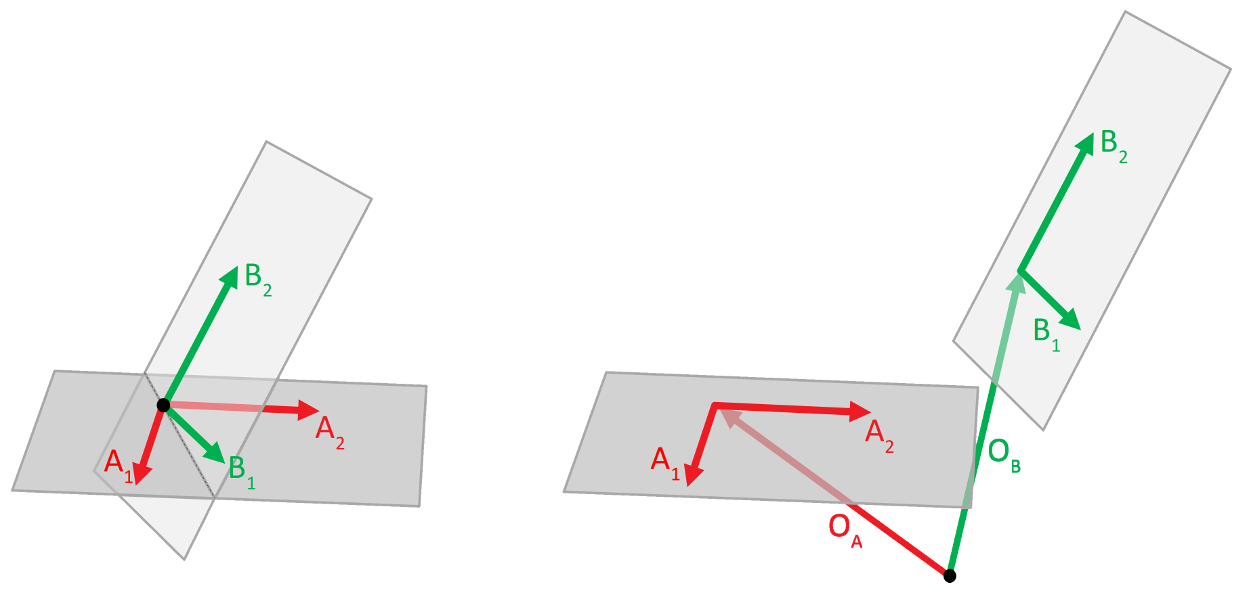
On the left hand side, the two planes A and B are shown as used with the signature (1) of align(). The basis vectors of both planes are defined from the global origin (black spot). Both planes cross at this point. The right shows the situation for the second signature of the function. Vectors OA (originA) and OB (originB) are used to define the positions of two arbitrarily placed planes.
Remark
The transformation returned by this function does not scale nor does it alter angles. This means, it is a combination of a translation and a rotation (i.e. a rigid transformation).
The example implements a function that creates a mapping transformation from an arbitrary plane onto the X-Y plane:
Example
#import ( "std/align_planes.sps" )
function align_xy( vector vecA1, vector vecA2, vector originA )
{
return align_planes::align( vecA1, vecA2, originA, <[1, 0]>, <[0, 1]>, <[0, 0]> )
}
The next example shows a function that uses six on-plane points to define planes A and B instead of the definiton by basis vectors:
Example
#import ( "std/align_planes.sps" )
function align_pts( vector a1, vector a2, vector a3, vector b1, vector b2, vector b3 )
{
return align_planes::align( a2 - a1, a3 - a1, a1, b2 - b1, b3 - b1, b1 )
}
Return value
An affine transformation from plane A to plane B.
Parameters
- vecA1
-
A (non-zero) vector on the initial plane A. This should be non-linear to vecA2.
- vecA2
-
A (non-zero) vector on the initial plane A. This should be non-linear to vecA1.
- originA
-
A space point defining the origin of the inital plane A. If this is not given, the global origin (<[0,0,0]>) is assumed.
- vecB1
-
A (non-zero) vector on the target plane B. This should be non-linear to vecB2.
- vecB2
-
A (non-zero) vector on the target plane B. This should be non-linear to vecB1.
- originB
-
A space point defining the origin of the target plane B. If this is not given, the global origin (<[0,0,0]>) is assumed.