Transformations
Transformations are a type of modifiers that are used to move or distort solid object or vectors in space. This page introduces the most imporant transformation types and explaines their usage.
Identity transformations
The identity transformation is the most simple transformation that does effectively nothing at all. It is used in cases where the declaration of a transformation or modifier is required even if no transformation is desired. One example would be functions with an obligatory transformation or modifier argument as input. An identity transformation can be accessed via the identity constructor:
Example
make identity() >> box()
Translation transformations
A translation transformation shifts a solid or a vector for a certain distance in one direction in space. The distance and direction are combined to the translation vector. In the corresponding translation constructor, the translation vector is given as argument of type vector. The following example creates a box that gets shifted by two units into the X direction:
Example
make translation( <[2.0,0.0,0.0]> ) >> box()
Rotation transformations
Rotations cause geometric entities to spin around a given axis. In trCAD, rotations generally follow the right-hand rule that defines their movement direction. Negative angle values can be used to spin into the opposite direction.
There are two rotation constructors available for defining a rotation transformation. The first one is of type rotation( vector, float ). It rotates the object around the axis given as first argument for an angle given as second argument. For this constructor, the rotation axis starts at the origin of the coordinate space.
Example
box b( 1.5, 2.0, 0.0, 0.9, 0.0, 0.1 )
make rotation( <[ 0.0, 0.0, 1.0 ]>, rad( 40 ) ) >> b
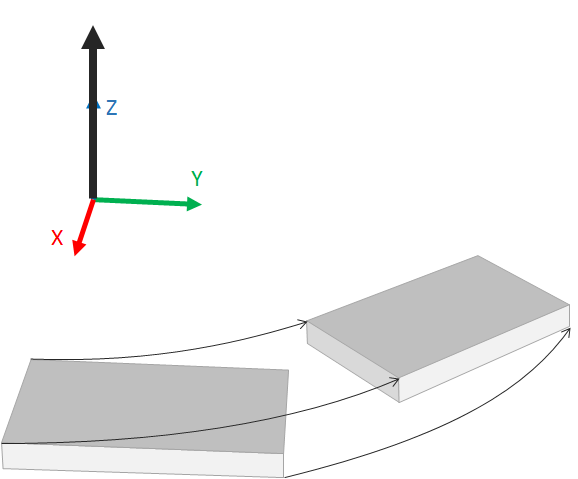
A rotation of 40 degree around the rotation axis (big black arrow) that is centered at the coordinate space origin.
The second constructor has the form rotation( vector, vector, float ). The first vector sets an onset point for the rotation axis (purple vector in the figure) while the second vector defines the rotation axis direction (big black arrow in the figure). This allows to turn any object around any arbitrary axis. The float parameter still defines the spinning angle.
Example
box b( 1.5, 2.0, 0.0, 0.9, 0.0, 0.1 )
make rotation( <[ 1.75, 0.45, 0.0 ]>, <[ 0.0, 0.0, 1.0 ]>, rad( 40 ) ) >> b
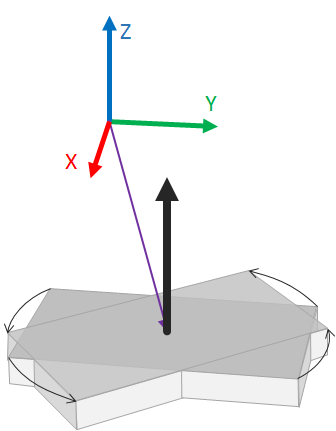
A rotation of 40 degree around the rotation axis (big black arrow) that is shifted into the object by the purple arrow.
Note
In trCAD, all angles are given in radians. The function rad() can be used to convert degrees into radiants.
Scaling and mirror transformations
Another basic transformation is the scaling of an object. There are four constructors for scaling: one for scaling uniformly into all directions, one for scaling unevenly into the three coordinate directions X, Y and Z and two constructors for scaling around a shifted coordinate offset. The first constructor simply takes one floating point value as an argument. It applies a uniform scaling with this scaling value:
Example
make scaling( 2.0 ) >> sphere()
The second constructor is used for non-uniform scaling. It accepts three floating point values, one for each direction:
Example
make scaling( 2.0, 1.0, 0.5 ) >> sphere()
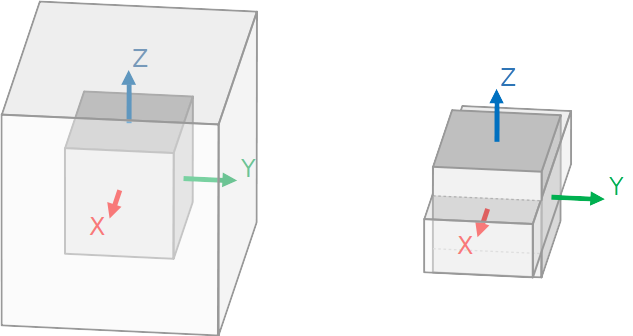
A uniform scaling (left) and non-uniform scaling (right) of a cube.
Please note that the application of uneven scaling constructors distorts the solid's original shape.
One or two negative values in this constructor can be used to mirror (or reflect) the geometric object along one or two major directions:
Example
make scaling( -1.0, 1.0, 1.0 ) >> mesh("bunny.stl")

The Stanford bunny and its mirrored version.
Scaling with these two constructors always leads to a scaling around the coordinate system origin. That means that the origin is the one point that stays in place when applying the scaling transformation. However it is often useful to keep a different point at a fixed poisiton. For this, two more constructors exist that are versions of the first scaling constructors but that take an additional vector as first argument. This defines the scaling center position that will not move during scaling:
Example
make scaling( <[ 0.5, 0.5, 0.5 ]>, 2.0 ) >> box()
make scaling( <[ 0.5, 0.5, 0.5 ]>, 0.5, 1.0, 3.0 ) >> box()
Affine transformations
What was not mentioned so far is that described commands translation, rotation and scaling are in fact constructors for a special data type atrafo. This stands for affine transformations and describes a class of transformations that contains the mentioned transformations.
Affine transformations can generally be expressed as 3x4 transformation matrices. Beside the above mentioned constructors there is also a direct constructor atrafo that accepts a matrix. This allows to define general affine transformations that are neither rotations, translations or scalings. These could be e.g. shearing transformations:
Example
make atrafo( <[<[ 1.0, 1.0, 0.0, 0.0 ]>,
<[ 0.0, 1.0, 0.0, 0.0 ]>,
<[ 0.0, 0.0, 1.0, 0.0 ]>]> ) >> mesh("bunny.stl")

A shearing affine transformation applied to the Stanford bunny.
(Note that another transformation boxwarp exists that also allows to apply shearing operations.)
Other transformations
Some more transformations exist like bending, boxwarp, helix or warp. These are described with more details in the reference section of this manual.