Solid Boolean Operations
One important way for editing solids is to apply solid boolean operations (see https://en.wikipedia.org/wiki/Constructive_solid_geometry ). Unlike the boolean operations that were described in the chapter about logical operators, these boolean operations act on solid objects and not on plain true / false values. The connection between the two becomes clearer when looking at a possible definition of the solid boolean operations:
A solid boolean operation between two solids A and B is equal to a certain logical boolean operation that is applied to every space point with the following rule: the logical value at one space point for solid A, B or the result is taken to be true if the space point lies inside the volume of A, B or the result and false if it lies outside of the volume of A, B or the result.
Lets demonstrate this for two overlapping solids A and B at four different space points p1, p2, p3 and p4 that are marked in the following image:
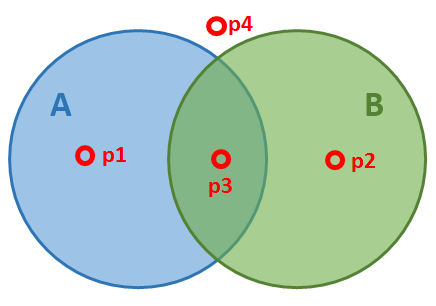
Solids A and B with points p1, p2, p3 and p4.
This table shows the logical boolean values for each of the four points that can be derived from the above definition:
| A | B | |
| p1 | true | false |
| p2 | false | true |
| p3 | true | true |
| p4 | false | false |
There are three most important solid boolean operations: intersection, union and difference. They correspond to the three boolean operations AND, OR and AND NOT. The last one, difference resp. AND NOT can be applied in two directions, either as A difference to B or as B difference to A, what makes actually four solid boolean operations in total. The following table shows the logical result of these four operations at the four points:
| intersection | union | difference | difference | |
| (A AND B) | (A OR B) | (A AND (NOT B)) | (B AND (NOT A)) | |
| p1 | false | true | true | false |
| p2 | false | true | false | true |
| p3 | true | true | false | false |
| p4 | false | false | false | false |
Applying this to all point in 3D space yields solid objects of a new shape that are the results of the solid boolean operations:

Results of the four most important boolean operations for solids A and B.
Solid Boolean Operators
As can be seen, operation intersection is based on the logical operation AND while operations union and difference behave pretty much the same way as one would expect for the arithmetic terms "addition" and "subtraction". For this reason, the solid boolean operators are
| & | + | - |
| &= | += | -= |
for "intersection", "union" and "difference" (with their assignment versions in the second row). This is depicted by the following examples:
Example
solid b = box()
solid c = translation(<[-0.2,-0.2,0.5 ]>) >> cylinder( <[1.4,1.4,0.0]>, 0.3 )
make b & c
Example
solid b = box()
solid c = translation(<[-0.2,-0.2,0.5 ]>) >> cylinder( <[1.4,1.4,0.0]>, 0.3 )
make b + c
Example
solid b = box()
solid c = translation(<[-0.2,-0.2,0.5 ]>) >> cylinder( <[1.4,1.4,0.0]>, 0.3 )
make b - c
that results in the following three objects:

Intersection, union and difference as derived from the examples.
Note
An important requirement for boolean operations to work well is that both input solids are water-tight meshes and not self-intersecting. This is especially important when working with external meshes.
Pseudo-Union Operator
There may be cases when two solids shall be added together without the complex procedure of a "real" boolean union. Then, a "pseudo-union" can be applied that combines the surfaces of the two solids as they are. The pseudo-union operator is
| (+) |
| (+)= |
Example
make box() (+) sphere()
Pseudo-unions are very fast and stable since they only join the solid without "fusing" them. However they can generator nested shells and self-intersecting solid and its up to the user to avoid errors that may follow from that.